SOFT MATTER RESEARCH
In the soft matter area, we focus on understanding glass and
jamming transitions in granular materials, dense colloidal suspensions,
foams, and model systems, in which the structural and stress
relaxation times diverge (in the absence of crystallization) when various control parameters such as temperature, density, and applied stress are tuned. We employ a combination of theoretical (master-equation approaches and statistical mechanics) and computational (molecular dynamics and Monte Carlo simulations) techniques to understand fundamental aspects of glass and jamming transitions.
Ongoing projects include:
1. Quasi-one dimensional models for glassy behavior
Dense colloidal suspensions undergo a glass transition as they are
compressed above the packing fraction φg = 0.58. For φ> φg, the viscosity diverges at such a stupendous rate that it
becomes experimentally impossible to measure. The nature of the
viscosity divergence (or equivalently the vanishing of particle
diffusion) as φ → φg is one of the fundamental open
questions in soft matter research. Related questions include at which
packing fraction does the viscosity truly diverge, does it depend on
quench rate, and what is the form of the divergence? To address these
questions, we have developed a quasi-one-dimensional model, where hard
rods diffuse through a series of connected loops and intersections.
The advantage of this model is that it displays many of the hallmarks of
the glass transition, yet the form of the divergence of the structural
relaxation with increasing packing fraction can be calculated
analytically. The analytical technique relies on a master equation
approach, where we define the relevant microstates of the system,
and then relate entropic bottlenecks to transition probabilities.
 |
 |
|---|---|
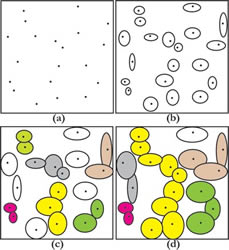
(a) Trajectory taken from molecular dynamics simulations of hard disks over a period in which the focus particle explores three cages α, β, and γ. The cage-entrance times are
provided. The red circles correspond to snapshots in (b)-(f), which are labeled by time. The focus particle is outlined in red and particles forming the α (β) cage are outlined in blue (green). |
Quasi-1D model with two intersections that displays several features of glassy dynamics including kinetic arrest and aging. |
Representative Publications:
(a) P. Pal, C. S. O'Hern, J. Blawzdziewicz, E. R. Dufresne, and R. Stinchcombe, ``A minimal model for kinetic arrest'', Phys. Rev. E 78 (2008) 011111.
(b) P. Pal, C. S. O'Hern, and J. Blawzdziewicz, "Quasi-one-dimensional models for glassy dynamics," submitted to Physical Review E (2010).
2. The connection between percolation in configuration space
and glassy dynamics
We have identified a link between the glass transition and percolation of regions of mobility in configuration space. We find that many hallmarks of glassy dynamics, for example stretched-exponential response functions and a diverging structural relaxation time, are consequences of the critical properties of mean-field percolation. Specific predictions of the percolation model include the range of possible stretching exponents 1/3 ≤ β ≤ 1 and the functional dependence of the structural relaxation time τα and exponent β on temperature, density, and wave number.
 |
|---|
Schematic of allowed regions in
configuration space for hard spheres. (a) At φJ only collectively jammed (CJ) states (points) are allowed; (b) At φ1 ≤ φJ motion occurs in closed mobility domains surrounding CJ states; (c) At φ2<φ1 transitions between contacting mobility domains (shaded) occur; (d) At φP < φ2 at least one network of mobility domains percolates (shaded yellow) and the system transitions from a glass to a metastable liquid. |
Representative Publications:
(a) G. Lois, J. Blawzdziewicz, and C. S. O'Hern, ``A percolation model for glassy dynamics in disordered materials'', Phys. Rev. Lett. 102 (2009) 015702.
(b) G. Lois, J. Blawzdziewicz, and C. S. O'Hern, ``Protein folding on rugged energy landscapes: Conformational diffusion on a fractal network'', submitted to Phys. Rev. E (2010).
3. Statistical mechanics of static and slowly flowing granular media
There is currently no fundamental understanding of how to uniquely characterize the state of a dense granular system using macroscopic descriptors. In this proposed research, we seek such a description using a systematic, bottom-up approach. We propose a set of coordinated experiments, numerical simulations, and theoretical studies to provide predictive and quantitative descriptions of the structural and mechanical properties of static and slowly driven granular materials. We will decompose granular packings into a collection of subsystems and measure their statistics. We will then correlate the statistics of the subsystems
with the measured structural and mechanical properties of the
packings, such as, packing fraction, contact number, radial
distribution function, and elastic moduli. These correlations will
provide a basis for a predictive theory of static and slowly driven
granular materials. In contrast to previously employed
quasi-thermodynamic approaches, we advocate using a master-equation
approach with no built-in assumptions about the packings
probabilities. Instead, we will develop a novel method to calculate
the packing probabilities of large systems in terms of the statistics
of small subsystems. This work will be done in collaboration
with Prof. Jerzy Blawzdziewicz (Mechanical Engineering, Physics) and
Prof. Mark Shattuck (Physics, Benjamin Levich Institute and CCNY).
Representative Publications:
(a) G.-J. Gao, J. Blawzdziewicz, and C. S. O'Hern, ``Geometrical families of mechanically stable granular packings,'' Phys. Rev. E 80 (2009) 061303.
(b) G.-J. Gao, J. Blawzdziewicz, C. S. O'Hern, and M. Shattuck, ``Experimental demonstration of nonuniform frequency distributions of mechanically stable granular packings'', Phys. Rev. E 80 (2009) 061304.
4. Jamming in systems composed of anisotropic particles and with polymer constraints
More than ten years ago, Andrea Liu (Physics, UPenn) and Sid Nagel (Physics, UChicago) introduced the provocative idea
that jamming behavior in athermal systems such as granular media and
foams has the same physical origin as glass transitions in thermal
systems. After a decade of intense study, there is
evidence that such a link exists at least for model particulate
systems composed of spherical particles. Moreover, we
now have a deeper understanding of the vibrational modes and
structural and mechanical properties for amorphous packings of
spherical particles.
However, there has been a relative paucity of work aimed at
investigating the structural, mechanical, and dynamical properties of
systems composed of objects with more realistic shapes and more
complex microstructures. In this research area, we will take the field of
jamming in two new directions that will enable even closer contact
with physical experiments over a wider range of systems. We will
perform novel theoretical and computational studies of (1) the
packing, slow dynamics, and mechanical response of systems composed of
frictionless, nonspherical particles and (2) the structure and
dynamics of polymer packings. These studies will lead to a deeper
understanding of soft matter systems such as granular media, foams,
emulsions, and colloids that undergo jamming and glass transitions.
Further, it will have a transformative impact on the research
communities that study polymer collapse and protein folding since the
tools and concepts from jamming and packing studies have not yet been
utilized in these areas.
 |
 |
|---|---|
Image of stress chains in a system of compressed photoelastic
ellipses. Bright ellipses experience much larger stresses than dark ones. Graphic courtesy of Prof. Bob Behringer, Duke University. | Mechanically stable packing of bidisperse ellipse-shaped particles. |
 |
 |
|
|---|---|---|
Sample configurations of model collapsed polymers. Both are obtained from molecular dynamics simulations of a quench from high to zero temperature. The left image shows the end state of a rapid quench; the system has a crystalline inner core and disordered exterior. When the quench is 10,000 times slower, as in the right image, the core is larger and the exterior more ordered. The colors of monomers indicate the number of nearest neighbors, with bright blue indicating close-packing. | ||
Representative Publications:
(a) M. Mailman, C. F. Schreck, B. Chakraborty, and C. S. O'Hern, ``Jamming in systems composed of ellipse-shaped particles'', Phys. Rev. Lett. 102 (2009) 255501.
(b) C. Schreck and C. S. O’Hern, “A comparison of jamming behavior in systems composed of dimer and ellipsoidal shaped particles,” submitted to Soft Matter (2010).